Hình chữ nhật là một hình quen thuộc trong đời sống và được ứng dụng rộng rãi hằng ngày. Các bạn học sinh cũng đã được làm quen với Hình chữ nhật từ cấp 1, từ các hình dán, vẽ cơ bản đến các khối lắp ghép phức tạp, ngay đến bộ bàn ghế ngồi học cũng thiết kế theo Hình chữ nhật… Vậy đâu là khái niệm, tính chất và cách chứng minh Tứ giác là Hình chữ nhật mà các bạn cần chú ý để tiếp thu và giải bài tập được tốt hơn? Hãy cùng Gia Sư Việt khám phá qua bài viết dưới đây nhé !
Mục lục
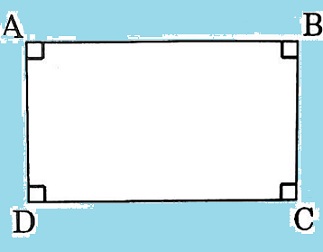
I. Khái niệm về Hình chữ nhật
Hình chữ nhật là Tứ giác có bốn góc vuông.
Từ khái niệm và hình vẽ trên, ta có: Nếu ABCD là Hình chữ nhật thì Góc A = B = C = D = 90°
II. Các tính chất của Hình chữ nhật
Hình chữ nhật là có tất cả các tính chất của hình bình hành và hình thang cân.
– Tính chất 1: Trong hình chữ nhật, các cạnh đối bằng nhau.
Ví dụ: Hình chữ nhật ABCD => AB = CD và AD = BC
– Tính chất 2: Trong hình chữ nhật, các góc đối bằng nhau.
Ví dụ: Hình chữ nhật ABCD => Góc A = B = C = D = 90°
III. Các định lí quan trọng về Hình chữ nhật
– Định lí 1: Trong Hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Ngược lại, nếu tứ giác có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
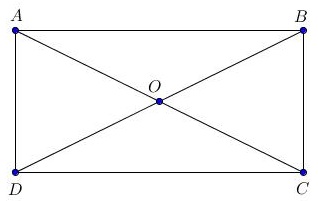
Ví dụ: Cho tứ giác ABCD có AC = BD và cắt nhau tại O, trong đó OA = OB = OC = OD, chứng minh Tứ giác ABCD là Hình chữ nhật.
Xét tam giác ABD có:
OA = OB = OD (gt) => ∆ABD vuông tại A
( Tính chất đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền trong tam giác vuông )
Chứng minh tương tự, ta có:
∆ABC vuông tại B, ∆BCD vuông tại C, ∆CDA vuông tại D
=> Tứ giác ABCD là hình chữ nhật do có 4 góc vuông.
– Định lí 2: Áp dụng vào Tam giác
+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
Ví dụ: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.
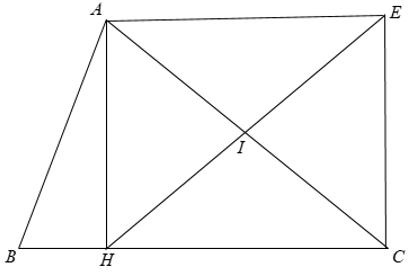
Xét Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = ½AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = ½ HE ⇒ Δ HCE vuông tại C.
Chứng minh tương tự ta có: Δ AHE, Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có Góc EAH = AHC = HCE = CEA = 90°
⇒ Tứ giác AHCE là hình chữ nhật. ( đ.p.c.m )
IV. Cách chứng minh Tứ giác là Hình chữ nhật
Cách 1: Tứ giác có ba góc vuông
Ví dụ: Cho tứ giác ABCD có ∆ABC vuông tại A,∆BCD vuông tại B, ∆CDA vuông tại C. Tứ giác ABCD là hình gì. Vì sao?
Theo bài ra, ta có:
∆ABC vuông tại A => Góc BAC = 90°
∆BCD vuông tại B => Góc CBD = 90°
∆CDA vuông tại C => Góc DCA = 90°
=> Góc ADC = 90° (Tổng 4 góc của một tứ giác bừng 360 độ)
=> Tứ giác ABCD là hình chữ nhật do có bốn góc vuông. ( đ.p.c.m )
Cách 2: Hình thang cân có một góc vuông
Ví dụ: Cho hình thang cân ABCD với AB // CD, giả sử góc D = 90°. Chứng minh ABCD là hình chữ nhật
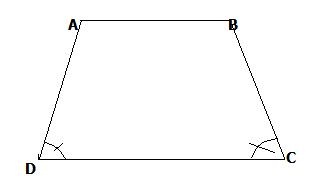
Theo giả thiết: Góc D = 90°
Ta có: AB // CD (ABCD là hình thang)
=> Góc A + D = 180° (hai góc trong cùng phía)
=> Góc A = 90°
Lại có Góc A + Góc C = 180° => Góc C = 90°
Vậy tứ giác ABCD có 3 góc A = B = C = 90°
=> ABCD là Hình chữ nhật. ( đ.p.c.m )
Cách 3: Hình bình hành có một góc vuông
Ví dụ: Cho tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM // BC (M thuộc AB). Chứng minh tứ giác PCQM là hình chữ nhật.
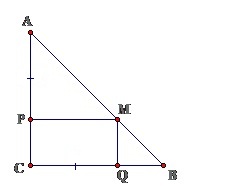
Theo bài ra, ta có:
∆ABC vuông tại C => AC ⊥ BC = > AP ⊥ PM
=> ∆APM vuông cân tại P
=> AP = PM
Lại có: AP = CQ
Mà PM // CQ
=> MNPQ là hình bình hành (1)
Mặt khác: Góc C = 90° (2)
Từ (1) và (2) => Tứ giác MNPQ là hình chữ nhật ( đ.p.c.m )
Cách 4: Hình bình hành có hai đường chéo bằng nhau
Ví dụ: Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
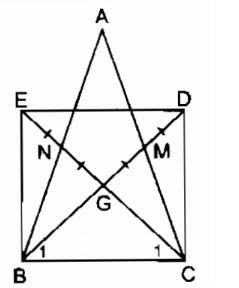
Theo bài ra, ta có: G là trọng tâm của ΔABC.
⇒ GB = 2GM và GC = 2GN
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (3)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (4)
Từ (3) và (4) ⇒ Tứ giác BCDE là Hình bình hành do hai đường chéo cắt nhau tại trung điểm mỗi đường. (5)
Xét ΔBCM và ΔCNB, có:
BC cạnh chung
Góc BCM = CBN (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ΔBCM = ΔCBN (c.g.c)
⇒ Góc B1 = C1 ⇒ ΔGBC cân tại G ⇒ GB = GC ⇒ BD = CE (6)
Từ (5) và (6), suy ra: BCDE là hình chữ nhật do là hình bình hành có hai đường chéo bằng nhau. ( đ.p.c.m )
Lời kết: Vậy là các khái niệm, tính chất và cách chứng minh Tứ giác là Hình chữ nhật đã được Gia Sư Việt phân tích rõ ràng ở trên. Với các ví dụ minh họa và bài tập chi tiết, hi vọng đây sẽ là nguồn tài liệu quý giá để các bạn làm bài và ôn thi hiệu quả. Ngoài ra, nếu cần tìm gia sư Toán đồng hành trong học tập, phụ huynh và học sinh vui lòng liên hệ qua số 096.446.0088 để được tư vấn và lựa chọn giáo viên, sinh viên dạy kèm phù hợp nhất.
Tham khảo thêm:
♦ Top 10 địa chỉ cung cấp gia sư tại quận Hoàng Mai uy tín nhất
♦ Khái niệm, tính chất và cách chứng minh Tứ giác là Hình vuông
♦ Khái niệm, tính chất & cách chứng minh Tứ giác là Hình bình hành

Để lại bình luận