Đối với phần Hình học, Tam giác là một hình tuy đơn giản nhưng nhiều bạn vẫn còn mơ hồ và chưa nắm được kiến thức cơ bản. Để giúp học sinh hiểu rõ hơn về nội dung này, Gia Sư Việt sẽ đem đến bài học về định nghĩa, định lý, tính chất và cách chứng minh các đường Đồng quy trong Tam giác. Chắc chắn đây sẽ là giải pháp hỗ trợ khá hiệu quả cho các em học sinh trong quá trình làm bài tập và kì thi quan trọng.
I. Đường phân giác
1. Tính chất của đường phân giác
Tính chất 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
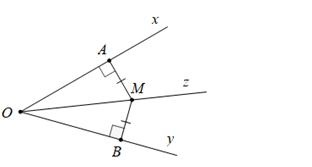
Từ hình vẽ, ta thấy:
M ∈ Oz
MA ⊥ Oy; MB ⊥ Oy
Dẫn đến: MA = MB, do hai tam giác vuông MOA = MOB
Tính chất 2: Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Theo hình trên: Nếu M nằm trong góc xOy và MA = MB thì M nằm trên tia phân giác Oz của góc xOy
2. Định lý về đường phân giác trong Tam giác
Định lí 1: Ba đường phân giác của một Tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của Tam giác đó.
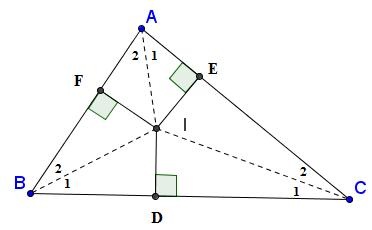
Từ hình vẽ, ta thấy: Tam giác ABC có 3 đường phân giác giao tại I. Khi đó:
Góc A1 = A2; Góc B1 = B2; Góc C1 = C2
Và ID = IE = IF
Định lí 2: Đường phân giác trong của một Tam giác chia cạnh đối diện thành hai đoạn thẳng tỷ lệ với hai cạnh kề với đoạn ấy.
*Lưu ý: Điều này cũng đúng với đường phân giác ngoài.
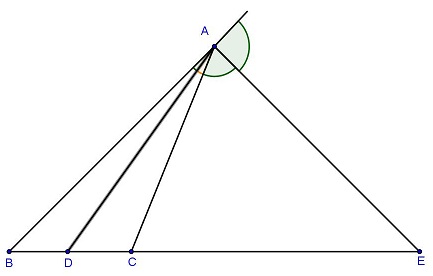
Từ hình vẽ, ta thấy:
DB/DC = AB/AC
EB/EC = AB/AC
*Chứng minh:
Qua đỉnh B vẽ đường thẳng song song với AC, cắt đường thẳng AD tại điểm E
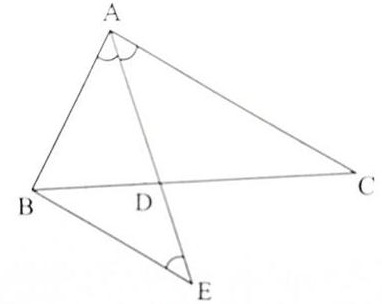
Ta có:
Góc BAE = Góc CAE (giả thuyết)
Vì BE // AC, nên Góc BEA = Góc CAE (so le trong)
Suy ra Góc BAE = Góc BEA . Do đó tam giác ABE cân tại B, suy ra:
BE = AB (1)
Áp dụng hệ quả của định lí Ta-let đối với tam giác DAC, ta có:
DB/DC = BE/AC (2)
Từ (1) và (2) suy ra: DB/DC = AB/AC
Như vậy, chân các đường phân giác trong và phân giác ngoài của một góc tại một đỉnh của tam giác là các điểm chia trong và chia ngoài các cạnh đối diện theo tỉ số bằng tỉ số của hai cạnh bên tương ứng: DB/DC = EB/EC = AB/AC
3. Cách chứng minh đường phân giác
– Cách 1: Chứng minh hai góc ở một đỉnh bằng nhau.
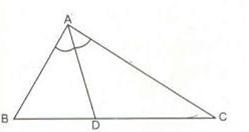
Ví dụ: Tam giác ABC có AD chia góc A thành hai góc BAD và góc CAD bằng nhau. => AD là đường phân giác tại đỉnh A của tam giác ABC
– Cách 2: Chứng minh hai đoạn thẳng đối diện tỷ lệ với hai cạnh kề với đoạn ấy.
Ví dụ: Tam giác ABC có DB/DC = AB/AC
=> AD là đường phân giác tại đỉnh A của tam giác ABC
– Cách 3 (Dùng trong trường hợp tam giác cân): Chứng minh đường đó là đường trung tuyến trong tam giác cân.
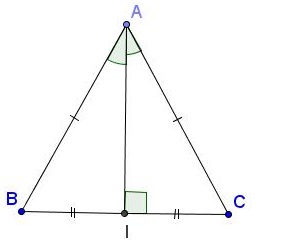
Ví dụ: Tam giác ABC cân có AD là đường trung tuyến => AD cũng đồng thời là đường phân giác tại đỉnh A của tam giác ABC
II. Đường trung trực
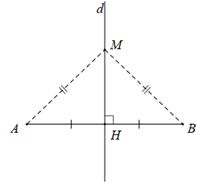
Định nghĩa: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
1. Tính chất đường trung trực
Tính chất 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Ví dụ: M thuộc đường trung trực của AB => MA = MB
Tính chất 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Ví dụ: MA = MB => M thuộc đường trung trực của AB
2. Định lý đường trung trực trong Tam giác
Định lí 1: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
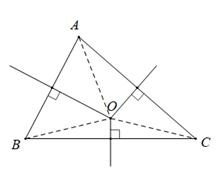
Từ hình vẽ, ta thấy:
Điểm O là giao điểm các đường trung trực trong ∆ABC
OA = OB = OC
=> O là tâm đường tròn ngoại tiếp ∆ABC
Định lí 2: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.
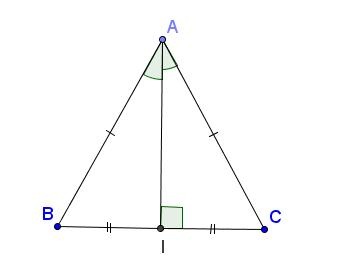
Ví dụ: ∆ABC có AD là đường trung tuyến của đáy
=> AD cũng đồng thời là đường trung trực tại đỉnh A của tam giác ABC
3. Cách chứng minh đường trung trực
– Cách 1: Chứng minh đường đó vuông góc với một cạnh của tam giác tại trung điểm.
Ví dụ: Tam giác ABC có AD ⊥ BC tại trung điểm của BC
=> AD là đường trung trực ứng với BC của tam giác ABC
– Cách 2: Chứng minh có một điểm cách nằm trên đường đó cách đều 2 cạnh bên.
Ví dụ: Tam giác ABC có điểm M ∈ AD, MA = MB
=> AD là đường trung trực tại đỉnh A của tam giác ABC
– Cách 3 (Dùng trong trường hợp tam giác cân): Chứng minh đường đó là đường trung tuyến trong tam giác cân
Ví dụ: Tam giác ABC cân có AD là đường trung tuyến
=> AD cũng đồng thời là đường trung trực ứng với đáy của tam giác ABC
III. Đường trung tuyến
Định nghĩa: Đường trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.
1. Định lý về đường trung tuyến trong Tam giác
Định lý 1: Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.
Định lý 2: Khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng ⅔ đường trung tuyến tương ứng với đỉnh đó.
Định lý 3: Khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng ⅓ đường trung tuyến tương ứng với điểm đó.
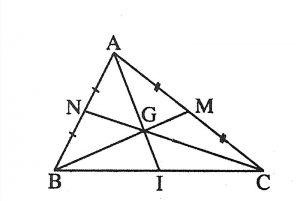
Ví dụ: Tam giác ABC có G là trọng tâm
AG = 2/3 AI; BG = 2/3 BM; CG = 2/3 CN
GI = 1/3 AI; GM = 1/3 BM; GN = 1/3 CN
2. Tính chất về đường trung tuyến
Tính chất 1: Trong tam giác cân (hoặc tam giác đều) đường trung tuyến ứng với cạnh đáy chia tam giác thành hai tam giác bằng nhau.
Ví dụ: Tam giác ABC cân có AD là đường trung tuyến
=> Diện tích ABD = ACD
Tính chất 2: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng ½ cạnh huyền.
Ví dụ: Tam giác ABC vuông tại A có AM là đường trung tuyến
=> AM = MB = MC = 1/2 BC
3. Cách chứng minh đường trung tuyến
– Cách 1: Chứng minh đường đó nối một đỉnh của tam giác với trung điểm cạnh đối diện.
Ví dụ: Tam giác ABC có D là trung điểm BC
=> AD là đường trung tuyến của tam giác ABC
– Cách 2: Chứng minh khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng ⅔ đường trung tuyến tương ứng với đỉnh đó.
Ví dụ: Tam giác ABC có điểm G thỏa mãn AG = 2/3 AD (D ∈ BC)
=> AD là đường trung tuyến của tam giác ABC
– Cách 3: Chứng minh khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng ⅓ đường trung tuyến tương ứng với điểm đó.
Ví dụ: Tam giác ABC có điểm G thỏa mãn GD = 1/3 AD (D ∈ BC)
=> AD là đường trung tuyến của tam giác ABC
IV. Đường cao
1. Tính chất về đường cao
Tính chất 1: Trong tam giác cân, đường cao tương ứng với cạnh đáy chính là đường trung tuyến ứng với cạnh đó, là đường phân giác của góc ở đỉnh và đường trung trực của đáy tam giác.
Ví dụ: Tam giác cân ABC có AI là đường cao
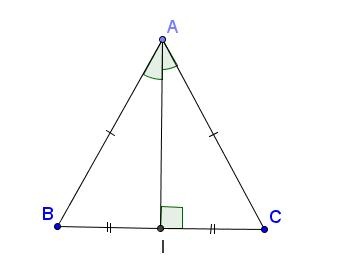
=> AI cũng là đường trung tuyến ứng với BC, tia phân giác góc A và đường trung trực của BC.
Tính chất 2: Trong tam giác vuông, đường cao với đáy là một cạnh góc vuông chính là cạnh góc vuông còn lại. Như vậy thì đỉnh góc vuông chính là chân đường cao hạ từ hai đỉnh còn lại xuống hai cạnh góc vuông của tam giác.
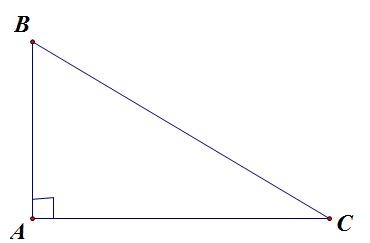
Ví dụ: Tam giác ABC vuông tại A
=> BA là đường cao ứng với AC, CA là đường cao ứng với AB
2. Định lý về đường cao trong Tam giác
Định lí 1: Ba đường cao của một tam giác đồng quy tại một điểm. Điểm đó gọi là trực tâm của tam giác.
Ví dụ: Cho hình vẽ sau. Chứng minh NS ⊥ ML
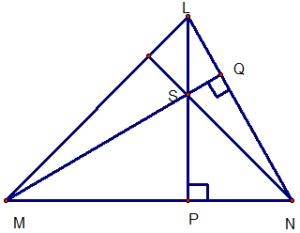
Xét ΔMNL, ta có:
LP MN (gt) => LP là đường cao thứ nhất.
MQ LN (gt) => MQ là đường cao thứ hai.
LP cắt MQ tại S.
=> S là trực tâm của ΔMNL
=> NS là đường cao thứ ba.
=> NS ⊥ ML
Định lí 2: Trong tam giác vuông, đường cao ứng với cạnh đáy chia tam giác thành hai tam giác đồng dạng.
Ví dụ: Tam giác ABC vuông tại A
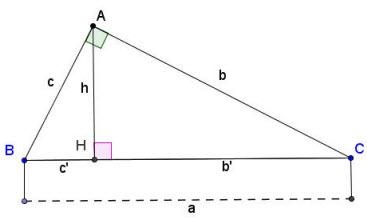
=> ΔABH ~ ΔACH
*Một số đẳng thức liên quan:
Đẳng thức bên trái: c2 = c’×a
Đẳng thức bên phải: b2 = b’×a
Đẳng thức ở giữa: h2 = b’×c’
3. Cách chứng minh đường cao
– Cách 1: Chứng minh đường đó vuông góc với một cạnh của tam giác.
Ví dụ: Tam giác ABC có AH ⊥ BC
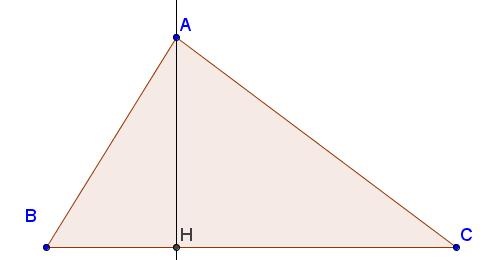
=> AH là đường cao của tam giác ABC
– Cách 2: Dùng định lí Py-ta-go hoặc các đẳng thức trong tam giác vuông
Ví dụ: Tam giác ABC có H thuộc BC, (BC)2 = (AB)2 + (AC)2
=> AH là đường cao ứng với BC
Ví dụ: Tam giác ABC vuông tại A, có (AH)2 = HB × HC
=> AH là đường cao ứng với BC
Lời kết: Mong rằng bài học trên đây về các đường đồng quy trong Tam giác sẽ giúp các bạn có một góc nhìn sâu và đa chiều hơn về hình học. Đồng thời cũng ghi nhớ các công thức và định lí cần thiết khi giải bài tập liên quan đến tam giác, Gia Sư Việt xin chúc các bạn tiếp thu và học tập hiệu quả nhất. Nếu bạn cần gia sư Toán hỗ trợ việc học tại nhà, vui lòng liên hệ chúng tôi qua số 096.446.0088 – 090.462.8800 để biết thêm chi tiết.
Tham khảo thêm:
♦ Định nghĩa, tính chất & cách chứng minh các Tam giác đặc biệt
♦ Khái niệm, tính chất & cách chứng minh Tứ giác là Hình bình hành
Thông tin rất hay và bổ ích
Bài tổng hợp rất đầy đủ, cảm ơn ad gia sư Việt nhiều ạ
Rất hay và bổ ích, cảm ơn Admin
Thông tin hay và bổ ích
Bài viết rất hay và bổ ích. Hình như còn 1 cách chứng minh đường phân giác nữa. Điểm cách đều 2 cạnh của tam giác thì nằm trên đường phân giác của góc đó
Hay và bổ ích
Rất hay và bổ ích. Đầy đủ thông tin về các trường hợp đồng quy của tam giác và ví dụ rõ ràng. Cảm ơn gia sư Việt.