Toán luôn là môn học khó nhằn với phần lớn học sinh, đặc biệt với chương trình lớp 12, nó được phân chia nhiều mảng kiến thức khác nhau. Một trong số đó là phần nội dung về khối đa diện của môn Hình học 12. Bài viết dưới đây sẽ tổng hợp một số khái niệm, công thức cơ bản cần nhớ về khối đa diện trong Toán 12. Các em học sinh đang cần ôn tập, luyện thi tốt nghiệm, đại học cùng tham khảo để nắm vững kiến thức này nhé.
Mục lục
I. Một số khái niệm cơ bản về Khối đa diện trong Toán 12
1. Định nghĩa về khối đa diện
Khái niệm khối đa diện: Hình H cùng các điểm nằm trong hình H được gọi là khối đa diện giới hạn bởi hình H. Lưu ý chỉ xét các hình H là hình đa diện gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện sau đây:
+) Hai đa giác bất kì hoặc là không có điểm chung hoặc là có một đỉnh chung hoặc là có 1 cạnh chung
+) Mỗi cạnh của 1 đa giác là cạnh chung của đúng hai đa giác.
2. Khối đa diện lồi và khối đa diện đều
Khối đa diện (H) được gọi là khối đa diện lồi khi đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó khối đa diện giới hạn (H) được gọi là đa diện lồi. Một khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
3. Khối đa diện lồi được gọi là khối đa diện đều loại { p,q } nếu:
+) Mỗi mặt của khối đa diện là một đa giác đều p cạnh.
+) Mỗi đỉnh của khối đa diện là đỉnh chung của đúng q mặt.
– Các mặt của khối đa diện đều là các đa giác đều và bằng nhau.
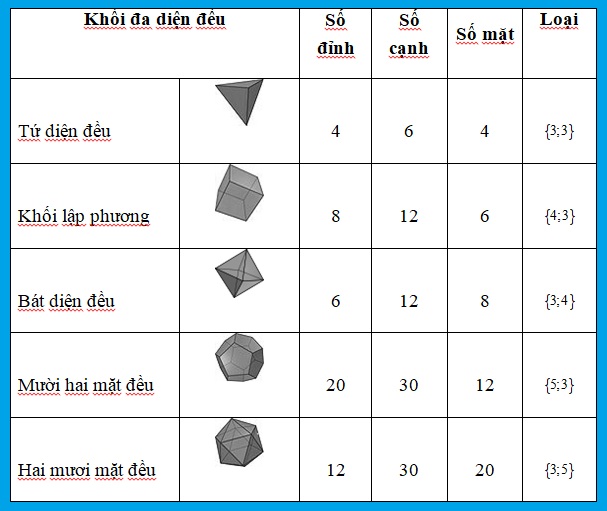
– Có năm loại khối đa diện đều, đó là khối đa diện đều loại {3,3}, loại {3,4}, loại {4,3}, loại {5,3}, và loại {3,5}.
– Hai khối đa diện đều có cùng số mặt và có cạnh bằng nhau thì bằng nhau.
– Hai khối đa diện đều có cùng số mặt thì đồng dạng với nhau.
II. Công thức cần nhớ về Khối đa diện trong Toán lớp 12
1. Khối đa diện đều loại {3,3}
Diện tích với cạnh đều là a: S = √3.a2
Thể tích với cạnh đều là a: V = √2.a3/12
Bán kính mặt cầu ngoại tiếp: R = √6.a/4
2. Khối đa diện đều loại {3,4}
Diện tích với cạnh đều là a: S = 2.√3.a2
Thể tích với cạnh đều là a: V = √2.a3/3
Bán kính mặt cầu ngoại tiếp: R = √6.a/2
3. Khối đa diện đều loại {4,3}
Diện tích với cạnh đều là a: S = 6a2
Thể tích với cạnh đều là a: V = a3
Bán kính mặt cầu ngoại tiếp: R = √3.a/2
Ở trên chỉ gồm công thức tính toán của mấy loại khối đa điện đơn giản, còn nhiều dạng phức tạp khác trong Toán lớp 12, bạn cần nắm vững các khái niệm, định nghĩa, tính chất để áp dụng giải bài tập. Hiện nay, chương trình học trên lớp không đủ giúp bạn giải thành thạo hết những dạng Toán nâng cao về khối đa diện. Vì vậy, bạn cần chăm chỉ ôn luyện và làm bài tập về nhà mới có thể hoàn thiện kĩ năng giải Toán phần này.
III. Cách giúp con tiếp thu kiến thức về Khối đa diện hiệu quả
Hiện nay, nhu cầu nâng cao kiến thức Toán ở tất cả bậc học, lớp học đều rất cao. Bởi môn Toán là một trong những môn học khó và có kiến thức nặng. Chỉ với thời gian trên lớp học sinh không thể nằm vững kiến thức và làm được các bài tập. Vì vậy, giải pháp học kèm 1 – 1 tại nhà với gia sư giúp cha mẹ hỗ trợ con hiệu quả nhất. Phụ huynh hãy liên hệ Gia Sư Việt để được hỗ trợ gia sư Toán lớp 12 giỏi và hết lòng vì con mình. Chúng tôi cam kết chất lượng như sau:
- Quý phụ huynh sẽ được tư vấn chi tiết để lựa chọn gia sư phù hợp với kiến thức và trình độ của con.
- Tất cả gia sư đều được phỏng vấn kĩ lưỡng, lý lịch rõ ràng và xuất trình giấy chứng minh thư hoặc thẻ sinh viên, bảng điểm chứng minh năng lực trong quá trình học tập.
- Gia đình học sinh không phải chi trả bất cứ khoản chi phí nào cho trung tâm giúp tiết kiệm tài chính tối đa nhưng vẫn đảm bảo về chất lượng.
- Trung tâm sẽ thường xuyên gọi điện tư vấn về tình hình giảng dạy của gia sư. Đổi người dạy ngay lập tức nếu gia đình không hài lòng.
Tham khảo thêm:
♦ Vai trò, ứng dụng của số Phức với môn Toán và trong đời sống
♦ Một số công thức Hình Học môn Toán lớp 12 học sinh cần nhớ

Để lại bình luận